介绍

傅里叶变换是有史以来最 深刻的数学见解之一，但不幸的是，其含义深深地埋在了一些荒谬的方程式中。

傅立叶变换是一种将某些东西分解为一堆正弦波的方法。像往常一样，这个名字来自一个很久以前的数学家，叫做傅里叶。

用数学术语来说，傅立叶变换是一种将信号转换为其组成成分和频率的技术。

傅里叶变换不仅广泛用于信号（无线电，声音等）处理，而且还广泛用于图像分析（例如，傅里叶变换）。边缘检测，图像过滤，图像重建和图像压缩。一个例子：透射电子显微镜图像的傅立叶变换有助于检查样品的周期性。周期性-表示模式。数据的傅立叶变换可以扩展有关分析样品的可访问信息。为了更好地理解它，请考虑信号x（t）：

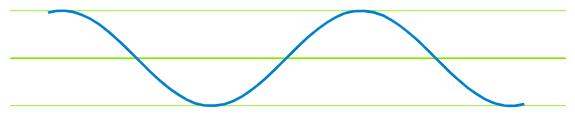
如果我们对另一个信号执行相同操作，并选择相同的时间点，我们将测量其幅度。

考虑另一个信号y（t）：

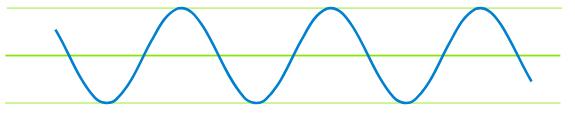
当我们同时发出这两个信号或将它们加在一起时会发生什么？

当我们在同一时间发射这两个信号时，我们得到一个新信号，它是这两个信号的振幅之和。之所以如此，是因为这两个信号被加在一起。

将两个信号相加：z（t）=x（t）+y（t）

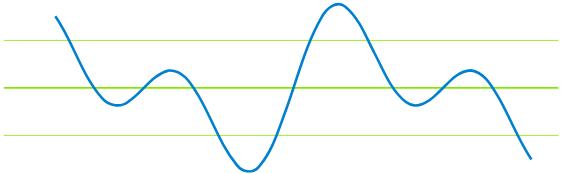
如果只给出一个信号（x（t）和y（t）之和），我们能否恢复原始信号x（t）和y（t）？

是。这就是傅立叶变换的作用。它吸收信号并将其分解为组成它的频率。

在我们的示例中，傅立叶变换会将信号z（t）分解成其组成频率，如信号x（t）和y（t）。

傅里叶变换的作用是将我们从时域移到频域。

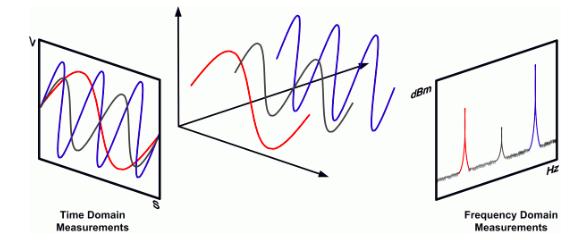
简洁透彻讲解傅立叶变换及其在AI中的应用

如果有人怀疑，我们是否要从频域回到时域呢？

我们可以使用傅立叶逆变换（IFT）来实现。

"时域中的任何连续信号都可以由无穷多个正弦波来唯一唯一地表示。"

这是什么意思？

这意味着，如果我们有某个函数生成的信号，则x(t)可以提出另一个函数，f(t)例如：

因此，无论信号有多强，我们都可以找到一个函数f(t)，该函数是无限多个正弦曲线之和，实际上可以完美地代表信号。

现在的问题是，如何在上式中找到系数，因为这些值将决定输出的形状，从而决定信号的形状。

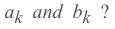
因此，为了获得这些系数，我们使用傅立叶变换，并且傅立叶变换的结果是一组系数。因此，我们X(w)用来表示傅立叶系数，它是频率的函数，是通过求解以下积分得到的：

傅立叶变换表示为不定积分：

X（w）：傅立叶变换x（t）：傅立叶逆变换

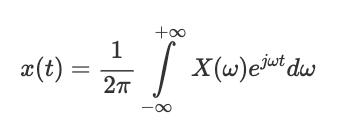
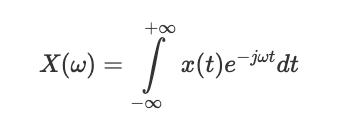
傅立叶变换和傅立叶逆变换

同样，当我们实际求解上述积分时，我们会在以下位置得到这些复数a并b对应于我们所要求的系数。

连续傅立叶变换将无限持续时间的时域信号转换成由无限数量的正弦波组成的连续频谱。实际上，我们处理的是离散采样的信号，通常以固定间隔，有限的持续时间或周期性地进行。为此，经典傅里叶变换算法可以表示为离散傅里叶变换（DFT），该函数将函数的等距样本的有限序列转换为离散时间的等距样本的等长序列傅里叶变换：

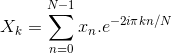
因此，这本质上是离散傅立叶变换。我们可以进行此计算，并且将产生一个复数，形式是我们在傅里叶级数中有两个系数a+ib

现在，我们知道了如何对信号进行采样以及如何应用离散傅立叶变换。我们希望做的最 后一件事是，我们想摆脱复数的i，因为它不支持的mllib或者systemML使用一些被称为欧拉公式的规定：

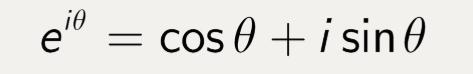
因此，如果将欧拉公式代入傅立叶变换方程并求解，它将产生实部和虚部。

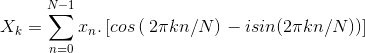
X由复数形式的a+ib或组成a-ib。因此，如果求解上述方程，将获得傅立叶系数a和b。

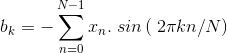
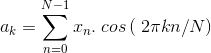
现在，如果只是将a和b的值放在等式中，f(t)则可以根据信号的频率定义信号。

在一般实践中，我们使用快速傅里叶变换（FFT）算法，该算法将DFT递归地划分为较小的DFT，从而大大减少了所需的计算时间。DFT的时间复杂度为2N²，而FFT的时间复杂度为2NlogN。

为什么表示信号时要使用余弦和正弦函数？

虽然正弦和余弦函数最 初是基于直角三角形定义的，但在当前情况下，从那种角度来看并不是最 好的事情。传统观点中正弦函数是"斜边对立的"，但是现在是时候有一点不同的观点了。

考虑单位圆：

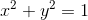
在笛卡尔平面上。假设通过原点的直线与轴在逆时针方向上形成角度θ，则直线与圆的交点为（cos⁡θ，sin⁡θ）。

想一想。这种观点与较早的观点相关吗？这两个定义是相同的。

假设我们通过使θ线性增加开始旋转直线。

正弦和余弦函数在某些情况下可以说是最 重要的周期函数：

SHM振荡器中位移，速度和加速度如何随时间变化的周期性函数是正弦函数。

2.每个粒子都有波动的性质，反之亦然。这是德布罗意的波粒对偶。波浪始终是某种物理量的正弦函数，例如EM波的电场和声波的压力。

声音本身就是压力扰动，它通过能够压缩和扩展的材料介质传播。与声波一起的一点处的压力随时间呈正弦变化。

傅立叶变换的收敛

如果一个点以恒定的速度绕圆运动，则其在地面上方的高度将跟踪正弦函数。点移动的速度对应于频率，圆的半径对应于振幅。

再增加1个圆圈，

再添加2个圆圈，

简洁透彻讲解傅立叶变换及其在AI中的应用

再添加9个圆圈：

简洁透彻讲解傅立叶变换及其在AI中的应用

几乎是离散的波形。

由于傅立叶定理，我们可以生成具有适当频率和半径的圆的任何信号。

人工智能中的傅立叶变换

傅立叶变换是线性函数，可引起非线性。使用卷积。

2个信号的乘积的傅立叶变换是2个信号的卷积。

令x（t）和y（t）是两个具有卷积X（t）*Y（t）的函数，而F表示傅立叶变换，则

F{x（t）.y（t）}=X（t）*Y（t）

请记住，时域中的卷积是频域中的乘法。这就是傅立叶变换主要用于机器学习，尤其是深度学习算法的方式。

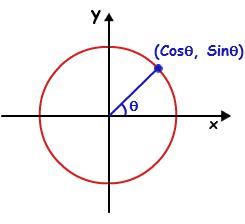
我将以卷积神经网络（CNN）为例；

CNN中90％的计算是卷积，并且有许多方法可以降低这种计算的强度，其中之一是快速傅立叶变换（FFT）。

代替卷积，输入和滤波器矩阵通过FFT转换到频域，以进行乘法。然后，通过逆FFT（IFFT）将输出转换回时域。

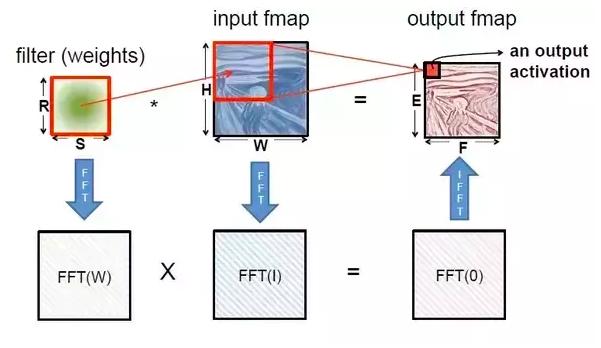
FFT的另一用途是可用于降维或特征提取。

当数据集中的每个样本都是信号（时间序列或图像等）时，它可能包含数千个样本。但是它们实际上可能只对应于傅立叶域中的几个点（特别是如果存在一定的周期性）。这大大简化了问题。

有时使用傅立叶域可能会提供平移不变性。也就是说，即使信号之间存在滞后，这种方差也不会影响它们在傅立叶域中的表示。

傅立叶变换的Python实现

可以使用numpy和scipypython库完成FFT的最 简单实现。

%matplotlibinline

importnumpyasnp

importmatplotlib.pyplotasplt

importscipy.fftpack

#Numberofsamplepoints

N=600

#samplespacing

T=1.0/800.0

x=np.linspace(0.0,N*T,N)

y=np.sin(50.0*2.0*np.pi*x)+0.5*np.sin(80.0*2.0*np.pi*x)

yf=scipy.fftpack.fft(y)

xf=np.linspace(0.0,1.0/(2.0*T),N/2)

fig,ax=plt.subplots()

ax.plot(xf,2.0/N*np.abs(yf[:N//2]))

plt.show()

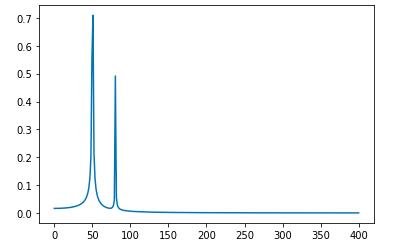
FFT图