1、对称加密算法
对称加密算法是应用较早的加密算法,数据发送方将明文和密钥经加密算法处理,使其变成密文发送出去;接收方收到密文后,使用和加密算法相同的密钥进行逆算法解密,还原出明文。在对称加密算法中,使用的密钥只有一个,收发双方使用相同的密钥对数据进行加密或解密。

双方都必须保管好密钥,任一方的密钥泄露,都会导致加密信息不安全;尤其是双方协商更换密钥过程中,密钥会出现在传输过程中,严重影响数据的安全性。
对称加密算法常用的AES可以参考嵌入式算法6---AES加密/解密算法。
2、非对称加密算法
和对称加密算法最大的区别是,非对称加密算法需要两个密钥,公开密钥(public key 简称公钥)和私有密钥(private key 简称私钥),且公钥与私钥是互相关联的一对。使用公钥对数据进行加密,只有用对应的私钥才能解密,私钥加密签名也只有公钥能解密验签。
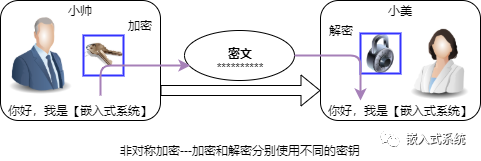
非对称加密算法实现机密信息交换的基本过程:
1、甲方生成一对密钥并将公钥公开,私钥保密
2、乙方使用甲方的提供的公钥,对机密信息加密后再发送给甲方;甲方使用自己私钥对加密后的信息进行解密
3、甲方也可以使用自己的私钥对机密信息进行签名后再发送给乙方,乙方用甲方的提供公钥对甲方发来的密文进行验签
非对称加密算法的特点:
1、公钥公开,私钥私藏,无需双方传输密钥协商,所以安全性比对称加密算法更高
2、非对称加密的算法复杂,运算速度比对称加密解密的速度慢很多
3、一般情况下使用非对称加密保护对称加密的密钥,密钥协商后使用对称加密进行通信
4、最佳实现是双方各自保存自己的私钥,使用对方的公钥加密数据传输
3、RSA算法与密钥
非对称加密算法中最常用的当属 RSA ,其算法本身基于一个简单的数论知识,给出两个素数,很容易将它们相乘,然而给出它们的乘积,想得到这两个素数就显得尤为困难。具体的私钥与公钥生成原理和加密、解密过程,不是本文关注的重点。
私钥和公钥的生成,可以借助mbedtls源码或openSSL工具生成,举例如下:
1、安装openSSL,下载地址
https://www.openssl.org/
2、安装后进入openSSL命令行界面,使用命令生成RSA2048的私钥,存入private.key文件
OpenSSL>genrsa -out private.key 2048
3、基于公钥生成私钥,存入文件public.key
OpenSSL> rsa -in private.key -pubout -out public.key
4、有些算法库采用传入指数、模数方式进行加解密,而前面生成的公私钥是PEM格式,需要变成Exponent、Modulus形式,就可以使用以下工具在线转换。
https://www.oren.net.cn/rsa/info.html
5、关于mbedtls应用,可以参考mbedtls 基础及其应用,该开源库适合嵌入式系统,且囊括了常用的各种算法。
4、源码
以下是RSA2048的C源码和验证范例,基于Qt测试,也可以结合硬件性能改为RSA1024,移植时注意适配形如 portable_***的三个API。
/************************************/
//关注微信公众号 嵌入式系统
/************************************/
//rsa.h
#include "stdlib.h"
#define RSA_ENCODE_LEN (2048/8) //RSA2048即256字节,可以视硬件情况改为1024
typedef unsigned char uint8_t;
typedef unsigned short int uint16_t;
typedef unsigned int uint32_t;
#define BI_MAXLEN 130
#define DEC 10
#define HEX 16
#define CARRYOVER 0x10000
#define CARRYLAST 0xFFFF
typedef struct
{
uint32_t m_nLength; //大数在0x1 00 00 00 00进制下的长度
uint16_t m_ulValue[BI_MAXLEN]; //用数组记录大数在0x100000000进制下每一位的值
} CBigInt;
//rsa.c
#include "rsa.h"
#include "time.h"
/******************* 适配API *******************/
#define portable_malloc malloc
#define portable_free free
//随机数种子源
uint32_t portable_rand_seed(void)
{
time_t timestamp;
time(×tamp);
return timestamp;
}
/******************* 适配API *******************/
/*****************************************************************
基本操作与运算
Init, 构造大数对象并初始化为零
Mov,赋值运算,可赋值为大数或普通整数,可重载为运算符“=”
Cmp,比较运算,可重载为运算符“==”、“!=”、“>=”、“<=”等
Add,加,求大数与大数或大数与普通整数的和,可重载为运算符“+”
Sub,减,求大数与大数或大数与普通整数的差,可重载为运算符“-”
Mul,乘,求大数与大数或大数与普通整数的积,可重载为运算符“*”
Div,除,求大数与大数或大数与普通整数的商,可重载为运算符“/”
Mod,模,求大数与大数或大数与普通整数的模,可重载为运算符“%”
*****************************************************************/
static CBigInt *Mov_Big_Long(CBigInt *X, uint32_t A);
static CBigInt *Mov_Big_Big(CBigInt *X, CBigInt *A);
static CBigInt *Add_Big_Big(CBigInt *X, CBigInt *A);
static CBigInt *Sub_Big_Big(CBigInt *X, CBigInt *A);
static CBigInt *Mul_Big_Big(CBigInt *X, CBigInt *A);
static CBigInt *Div_Big_Big(CBigInt *X, CBigInt *A);
static CBigInt *Mod_Big_Big(CBigInt *X, CBigInt *A);
static CBigInt *Add_Big_Long(CBigInt *X, uint32_t A);
static CBigInt *Sub_Big_Long(CBigInt *X, uint32_t A);
static CBigInt *Mul_Big_Long(CBigInt *X, uint32_t A);
static CBigInt *Div_Big_Long(CBigInt *X, uint32_t A);
static uint32_t Mod_Big_Long(CBigInt *N, uint32_t A);
static int Cmp(CBigInt *N, CBigInt *A);
/*****************************************************************
输入输出
Get,从字符串按10进制或16进制格式输入到大数
Put,将大数按10进制或16进制格式输出到字符串
*****************************************************************/
static CBigInt *Get(CBigInt *N, char *str, uint32_t system);
static char *Put(CBigInt *N, uint32_t system);
/*****************************************************************
RSA相关运算
Rab,拉宾米勒算法进行素数测试
Euc,欧几里德算法求解同余方程
RsaTrans,反复平方算法进行幂模运算
GetPrime,产生指定长度的随机大素数
*****************************************************************/
static int Rab(CBigInt *N);
static CBigInt *Euc(CBigInt *X, CBigInt *A);
static CBigInt *RsaTrans(CBigInt *X, CBigInt *A, CBigInt *B);
static CBigInt *GetPrime(CBigInt *X, int bits);
/*****************************************************************
大数运算库源文件:BigInt.c
说明:适用于C,linux系统 1024位RSA运算
*****************************************************************/
//小素数表
const static int PrimeTable[550] =
{
3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73,
79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179,
181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283,
293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419,
421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547,
557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661,
673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811,
821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947,
953, 967, 971, 977, 983, 991, 997, 1009, 1013, 1019, 1021, 1031, 1033, 1039, 1049, 1051, 1061, 1063, 1069, 1087,
1091, 1093, 1097, 1103, 1109, 1117, 1123, 1129, 1151, 1153, 1163, 1171, 1181, 1187, 1193, 1201, 1213, 1217, 1223, 1229,
1231, 1237, 1249, 1259, 1277, 1279, 1283, 1289, 1291, 1297, 1301, 1303, 1307, 1319, 1321, 1327, 1361, 1367, 1373, 1381,
1399, 1409, 1423, 1427, 1429, 1433, 1439, 1447, 1451, 1453, 1459, 1471, 1481, 1483, 1487, 1489, 1493, 1499, 1511, 1523,
1531, 1543, 1549, 1553, 1559, 1567, 1571, 1579, 1583, 1597, 1601, 1607, 1609, 1613, 1619, 1621, 1627, 1637, 1657, 1663,
1667, 1669, 1693, 1697, 1699, 1709, 1721, 1723, 1733, 1741, 1747, 1753, 1759, 1777, 1783, 1787, 1789, 1801, 1811, 1823,
1831, 1847, 1861, 1867, 1871, 1873, 1877, 1879, 1889, 1901, 1907, 1913, 1931, 1933, 1949, 1951, 1973, 1979, 1987, 1993,
1997, 1999, 2003, 2011, 2017, 2027, 2029, 2039, 2053, 2063, 2069, 2081, 2083, 2087, 2089, 2099, 2111, 2113, 2129, 2131,
2137, 2141, 2143, 2153, 2161, 2179, 2203, 2207, 2213, 2221, 2237, 2239, 2243, 2251, 2267, 2269, 2273, 2281, 2287, 2293,
2297, 2309, 2311, 2333, 2339, 2341, 2347, 2351, 2357, 2371, 2377, 2381, 2383, 2389, 2393, 2399, 2411, 2417, 2423, 2437,
2441, 2447, 2459, 2467, 2473, 2477, 2503, 2521, 2531, 2539, 2543, 2549, 2551, 2557, 2579, 2591, 2593, 2609, 2617, 2621,
2633, 2647, 2657, 2659, 2663, 2671, 2677, 2683, 2687, 2689, 2693, 2699, 2707, 2711, 2713, 2719, 2729, 2731, 2741, 2749,
2753, 2767, 2777, 2789, 2791, 2797, 2801, 2803, 2819, 2833, 2837, 2843, 2851, 2857, 2861, 2879, 2887, 2897, 2903, 2909,
2917, 2927, 2939, 2953, 2957, 2963, 2969, 2971, 2999, 3001, 3011, 3019, 3023, 3037, 3041, 3049, 3061, 3067, 3079, 3083,
3089, 3109, 3119, 3121, 3137, 3163, 3167, 3169, 3181, 3187, 3191, 3203, 3209, 3217, 3221, 3229, 3251, 3253, 3257, 3259,
3271, 3299, 3301, 3307, 3313, 3319, 3323, 3329, 3331, 3343, 3347, 3359, 3361, 3371, 3373, 3389, 3391, 3407, 3413, 3433,
3449, 3457, 3461, 3463, 3467, 3469, 3491, 3499, 3511, 3517, 3527, 3529, 3533, 3539, 3541, 3547, 3557, 3559, 3571, 3581,
3583, 3593, 3607, 3613, 3617, 3623, 3631, 3637, 3643, 3659, 3671, 3673, 3677, 3691, 3697, 3701, 3709, 3719, 3727, 3733,
3739, 3761, 3767, 3769, 3779, 3793, 3797, 3803, 3821, 3823, 3833, 3847, 3851, 3853, 3863, 3877, 3881, 3889, 3907, 3911,
3917, 3919, 3923, 3929, 3931, 3943, 3947, 3967, 3989, 4001
};
/****************************************************************************************
大数比较
调用方式:Cmp(N,A)
返回值:若N<A返回-1;若N=A返回0;若N>A返回1
****************************************************************************************/
static int Cmp(CBigInt *N, CBigInt *A)
{
int i;
if(N->m_nLength > A->m_nLength)
{
return 1;
}
if(N->m_nLength < A->m_nLength)
{
return -1;
}
for(i = N->m_nLength - 1; i >= 0; i--)
{
if(N->m_ulValue[i] > A->m_ulValue[i])
{
return 1;
}
if(N->m_ulValue[i] < A->m_ulValue[i])
{
return -1;
}
}
return 0;
}
/****************************************************************************************
大数赋值
调用方式:__Mov_Big_Big(A)
返回值:N,被赋值为A
****************************************************************************************/
static CBigInt *Mov_Big_Big(CBigInt *X, CBigInt *A)
{
memcpy(X, A, sizeof(CBigInt));
return X;
}
static CBigInt *Mov_Big_Long(CBigInt *N, uint32_t A)
{
int i;
if(A > CARRYLAST)
{
N->m_nLength = 2;
N->m_ulValue[1] = (uint16_t)(A >> 16);
N->m_ulValue[0] = (uint16_t)A;
}
else
{
N->m_nLength = 1;
N->m_ulValue[0] = (uint16_t)A;
}
memset((unsigned char*)&N->m_ulValue[N->m_nLength], 0, sizeof(uint16_t) * (BI_MAXLEN - N->m_nLength));
return N;
}
/****************************************************************************************
大数相加
调用形式:Add_Big_Big(X,A)
返回值:X=X+A
****************************************************************************************/
static CBigInt *Add_Big_Big(CBigInt *X, CBigInt *A)
{
uint32_t i;
uint16_t carry = 0;
uint32_t sum = 0;
if(X->m_nLength < A->m_nLength)
{
X->m_nLength = A->m_nLength;
}
for(i = 0; i < X->m_nLength; i++)
{
sum = A->m_ulValue[i];
sum = sum + X->m_ulValue[i] + carry;
X->m_ulValue[i] = (uint16_t)sum;
carry = (uint16_t)(sum >> 16);
}
X->m_ulValue[X->m_nLength] = carry;
X->m_nLength += carry;
return X;
}
static CBigInt *Add_Big_Long(CBigInt *X, uint32_t A)
{
uint32_t sum;
sum = X->m_ulValue[0];
sum += A;
X->m_ulValue[0] = (uint16_t)sum;
if(sum > CARRYLAST)
{
uint32_t i = 1;
while(X->m_ulValue[i] == CARRYLAST)
{
X->m_ulValue[i] = 0;
i++;
}
X->m_ulValue[i]++;
if(X->m_nLength == i)
{
X->m_nLength++;
}
}
return X;
}
/****************************************************************************************
大数相减
调用形式:Sub_Big_Big(X,A)
返回值:X=X-A
****************************************************************************************/
static CBigInt *Sub_Big_Big(CBigInt *X, CBigInt *A)
{
if(Cmp(X, A) <= 0)
{
memset(X, 0, sizeof(CBigInt));
return X;
}
else
{
uint16_t carry = 0;
uint32_t num;
uint32_t i;
for(i = 0; i < X->m_nLength; i++)
{
if((X->m_ulValue[i] > A->m_ulValue[i]) || ((X->m_ulValue[i] == A->m_ulValue[i]) && (carry == 0)))
{
X->m_ulValue[i] = X->m_ulValue[i] - carry - A->m_ulValue[i];
carry = 0;
}
else
{
num = CARRYOVER + X->m_ulValue[i];
X->m_ulValue[i] = (uint32_t)(num - carry - A->m_ulValue[i]);
carry = 1;
}
}
while(X->m_ulValue[X->m_nLength - 1] == 0)
{
X->m_nLength--;
}
return X;
}
}
static CBigInt *Sub_Big_Long(CBigInt *X, uint32_t A)
{
if(X->m_ulValue[0] >= A)
{
X->m_ulValue[0] -= A;
return X;
}
if(X->m_nLength == 1)
{
memset(X, 0, sizeof(CBigInt));
return X;
}
else
{
uint32_t num = CARRYOVER + X->m_ulValue[0];
int i = 1;
X->m_ulValue[0] = (uint16_t)(num - A);
while(X->m_ulValue[i] == 0)
{
X->m_ulValue[i] = CARRYLAST;
i++;
}
X->m_ulValue[i]--;
if(X->m_ulValue[i] == 0)
{
X->m_nLength--;
}
return X;
}
}
/****************************************************************************************
大数相乘
调用形式:Mul_Big_Big(N,A)
返回值:X=N*A
A a 0
N c d
0 d*0
1 c*0
d*a
2 c*a
****************************************************************************************/
static CBigInt *Mul_Big_Big(CBigInt *X, CBigInt *A)
{
if(A->m_nLength == 1)
{
return Mul_Big_Long(X, A->m_ulValue[0]);
}
else
{
uint32_t sum, mul = 0, carry = 0;
uint32_t i, j;
CBigInt N = {0};
memcpy(&N, X, sizeof(CBigInt));
memset(X, 0, sizeof(CBigInt));
X->m_nLength = N.m_nLength + A->m_nLength - 1;
for(i = 0; i < X->m_nLength; i++)
{
sum = carry;
carry = 0;
for(j = 0; j < A->m_nLength; j++)
{
if(((i - j) >= 0) && ((i - j) < N.m_nLength))
{
mul = N.m_ulValue[i - j];
mul *= A->m_ulValue[j];
carry += mul >> 16;
mul = mul & CARRYLAST;
sum += mul;
}
}
carry += sum >> 16;
X->m_ulValue[i] = (uint16_t)sum;
}
if(carry)
{
X->m_nLength++;
X->m_ulValue[X->m_nLength - 1] = (uint16_t)carry;
}
return X;
}
}
static CBigInt *Mul_Big_Long(CBigInt *X, uint32_t A)
{
uint32_t mul;
uint32_t carry = 0;
uint32_t i;
for(i = 0; i < X->m_nLength; i++)
{
mul = X->m_ulValue[i];
mul = mul * A + carry;
X->m_ulValue[i] = (uint16_t)mul;
carry = (uint16_t)(mul >> 16);
}
if(carry)
{
X->m_nLength++;
X->m_ulValue[X->m_nLength - 1] = carry;
}
return X;
}
/****************************************************************************************
大数相除
调用形式:Div_Big_Big(N,A)
返回值:X=N/A
****************************************************************************************/
static CBigInt *Div_Big_Big(CBigInt *X, CBigInt *A)
{
CBigInt Y = {0}, Z = {0}, T;
if(A->m_nLength == 1)
{
return Div_Big_Long(X, A->m_ulValue[0]);
}
else
{
uint32_t i, len;
uint32_t num, div;
memcpy(&Y, X, sizeof(CBigInt));
while(Cmp(&Y, A) >= 0)
{
div = Y.m_ulValue[Y.m_nLength - 1];
num = A->m_ulValue[A->m_nLength - 1];
len = Y.m_nLength - A->m_nLength;
if((div == num) && (len == 0))
{
Add_Big_Long(X, 1);
break;
}
if((div <= num) && len)
{
len--;
div = (div << 16) + Y.m_ulValue[Y.m_nLength - 2];
}
div = div / (num + 1);
Mov_Big_Long(&Z, div);
if(len)
{
Z.m_nLength += len;
for(i = Z.m_nLength - 1; i >= len; i--)
{
Z.m_ulValue[i] = Z.m_ulValue[i - len];
}
for(i = 0; i < len; i++)
{
Z.m_ulValue[i] = 0;
}
}
Add_Big_Big(X, &Z);
memcpy(&T, A, sizeof(CBigInt));
Mul_Big_Big(&T, &Z);
Sub_Big_Big(&Y, &T);
}
return X;
}
}
static CBigInt *Div_Big_Long(CBigInt *X, uint32_t A)
{
if(X->m_nLength == 1)
{
X->m_ulValue[0] = X->m_ulValue[0] / A;
return X;
}
else
{
uint32_t div, mul;
uint32_t carry = 0;
int i;
for(i = X->m_nLength - 1; i >= 0; i--)
{
div = carry;
div = (div << 16) + X->m_ulValue[i];
X->m_ulValue[i] = (uint16_t)(div / A);
mul = (div / A) * A;
carry = (uint16_t)(div - mul);
}
if(X->m_ulValue[X->m_nLength - 1] == 0)
{
X->m_nLength--;
}
return X;
}
}
/****************************************************************************************
大数求模
调用形式:Mod_Big_Big(N,A)
返回值:X=N%A
****************************************************************************************/
static CBigInt *Mod_Big_Big(CBigInt *X, CBigInt *A)
{
CBigInt Y = {0}, Z;
uint32_t div, num;
uint32_t carry = 0;
uint32_t i, len;
while(Cmp(X, A) >= 0)
{
div = X->m_ulValue[X->m_nLength - 1];
num = A->m_ulValue[A->m_nLength - 1];
len = X->m_nLength - A->m_nLength;
if((div == num) && (len == 0))
{
Sub_Big_Big(X, A);
break;
}
if((div <= num) && len)
{
len--;
div = (div << 16) + X->m_ulValue[X->m_nLength - 2];
}
div = div / (num + 1);
Mov_Big_Long(&Y, div);
memcpy(&Z, A, sizeof(CBigInt));
Mul_Big_Big(&Z, &Y);
memcpy(&Y, &Z, sizeof(CBigInt));
if(len)
{
Y.m_nLength += len;
for(i = Y.m_nLength - 1; i >= len; i--)
{
Y.m_ulValue[i] = Y.m_ulValue[i - len];
}
for(i = 0; i < len; i++)
{
Y.m_ulValue[i] = 0;
}
}
Sub_Big_Big(X, &Y);
}
return X;
}
static uint32_t Mod_Big_Long(CBigInt *N, uint32_t A)
{
if(N->m_nLength == 1)
{
return(N->m_ulValue[0] % A);
}
else
{
uint32_t div;
uint32_t carry = 0;
int i;
for(i = N->m_nLength - 1; i >= 0; i--)
{
div = N->m_ulValue[i];
div += carry * CARRYOVER;
carry = (uint16_t)(div % A);
}
return carry;
}
}
/****************************************************************************************
从字符串按10进制或16进制格式输入到大数
调用格式:Get(N,str,sys)
返回值:N被赋值为相应大数
sys暂时只能为10或16
****************************************************************************************/
static CBigInt *Get(CBigInt *N, char *s, uint32_t system)
{
int i;
int len = strlen(s), k;
memset(N, 0, sizeof(CBigInt));
N->m_nLength = 1;
for(i = 0; i < len; i++)
{
Mul_Big_Long(N, system);
if((s[i] >= '0') && (s[i] <= '9'))
{
k = s[i] - 48;
}
else if((s[i] >= 'A') && (s[i] <= 'F'))
{
k = s[i] - 55;
}
else if((s[i] >= 'a') && (s[i] <= 'f'))
{
k = s[i] - 87;
}
else
{
k = 0;
}
Add_Big_Long(N, k);
}
return N;
}
static CBigInt *GetHex(CBigInt *N, unsigned char *s, unsigned short len, uint32_t system)
{
int i, j;
unsigned char *p = (unsigned char*)N->m_ulValue;
memset(N, 0, sizeof(CBigInt));
N->m_nLength = 1;
for(i = len - 1, j = 0; i >= 0; i--, j++)
{
p[j] = s[i];
}
i = len % 2;
if(i > 0)
{
N->m_nLength = len / 2 + 1;
}
else
{
N->m_nLength = len / 2;
}
return N;
}
/****************************************************************************************
将大数按10进制或16进制格式输出为字符串
调用格式:Put(N,str,sys)
返回值:无,参数str被赋值为N的sys进制字符串
sys暂时只能为10或16
****************************************************************************************/
static char *Put(CBigInt *N, uint32_t system)
{
char t[17] = "0123456789ABCDEF";
int i, a;
static char s[2048];
if((N->m_nLength == 1) && (N->m_ulValue[0] == 0))
{
return NULL;
}
else
{
CBigInt X = {0};
memcpy(&X, N, sizeof(CBigInt));
memset(s, 0, 2048);
for(i = 2046; X.m_ulValue[X.m_nLength - 1] > 0 && i > 0; i--)
{
a = Mod_Big_Long(&X, system);
s[i] = t[a];
Div_Big_Long(&X, system);
}
if(i % 2 == 0)
{
return &s[i + 1];
}
else
{
s[i] = '0';
return &s[i];
}
}
}
static void PutHex(CBigInt *N, uint8_t *out, uint16_t *len)
{
int i, j, size;
if((N->m_nLength == 1) && (N->m_ulValue[0] == 0))
{
return;
}
size = N->m_nLength * sizeof(N->m_ulValue[0]);
for(i = size - 1, j = 0; i >= 0; i--, j++)
{
out[j] = ((uint8_t*)N->m_ulValue)[i];
}
*len = size;
}
/****************************************************************************************
求不定方程ax-by=1的最小整数解
调用方式:Euc(N,A)
返回值:X,满足:NX mod A=1
****************************************************************************************/
static CBigInt *Euc(CBigInt *X, CBigInt *A)
{
CBigInt M = {0}, E = {0}, N = {0}, Y = {0}, I = {0}, J = {0};
int x, y;
memcpy(&E, X, sizeof(CBigInt));
memcpy(&M, A, sizeof(CBigInt));
Mov_Big_Long(X, 0);
Mov_Big_Long(&Y, 1);
x = y = 1;
while((E.m_nLength != 1) || (E.m_ulValue[0] != 0))
{
memcpy(&I, &M, sizeof(CBigInt));
Div_Big_Big(&I, &E);
memcpy(&J, &M, sizeof(CBigInt));
Mod_Big_Big(&J, &E);
memcpy(&M, &E, sizeof(CBigInt));
memcpy(&E, &J, sizeof(CBigInt));
memcpy(&J, &Y, sizeof(CBigInt));
Mul_Big_Big(&Y, &I);
if(x == y)
{
if(Cmp(X, &Y) >= 0)
{
Sub_Big_Big(&Y, X);
}
else
{
Sub_Big_Big(&Y, X);
y = 0;
}
}
else
{
Add_Big_Big(&Y, X);
x = 1 - x;
y = 1 - y;
}
memcpy(X, &J, sizeof(CBigInt));
}
if(x == 0)
{
Sub_Big_Big(X, A);
}
return X;
}
/****************************************************************************************
求乘方的模
调用方式:RsaTrans(N,A,B)
返回值:X=N^A MOD B
****************************************************************************************/
static CBigInt *RsaTrans(CBigInt *X, CBigInt *A, CBigInt *B)
{
CBigInt N = {0}, Y = {0}, Z;
int i, j, k;
uint32_t n;
uint32_t num;
k = A->m_nLength * 16 - 16;
num = A->m_ulValue[A->m_nLength - 1];
while(num)
{
num = num >> 1;
k++;
}
memcpy(&N, X, sizeof(CBigInt));
for(i = k - 2; i >= 0; i--)
{
memcpy(&Y, X, sizeof(CBigInt));
Mul_Big_Long(&Y, X->m_ulValue[X->m_nLength - 1]);
Mod_Big_Big(&Y, B);
for(n = 1; n < X->m_nLength; n++)
{
for(j = Y.m_nLength; j > 0; j--)
{
Y.m_ulValue[j] = Y.m_ulValue[j - 1];
}
Y.m_ulValue[0] = 0;
Y.m_nLength++;
memcpy(&Z, X, sizeof(CBigInt));
Mul_Big_Long(&Z, X->m_ulValue[X->m_nLength - n - 1]);
Add_Big_Big(&Y, &Z);
Mod_Big_Big(&Y, B);
}
memcpy(X, &Y, sizeof(CBigInt));
if((A->m_ulValue[i >> 4] >> (i & 15)) & 1)
{
memcpy(&Y, &N, sizeof(CBigInt));
Mul_Big_Long(&Y, X->m_ulValue[X->m_nLength - 1]);
Mod_Big_Big(&Y, B);
for(n = 1; n < X->m_nLength; n++)
{
for(j = Y.m_nLength; j > 0; j--)
{
Y.m_ulValue[j] = Y.m_ulValue[j - 1];
}
Y.m_ulValue[0] = 0;
Y.m_nLength++;
memcpy(&Z, &N, sizeof(CBigInt));
Mul_Big_Long(&Z, X->m_ulValue[X->m_nLength - n - 1]);
Add_Big_Big(&Y, &Z);
Mod_Big_Big(&Y, B);
}
memcpy(X, &Y, sizeof(CBigInt));
}
}
return X;
}
/****************************************************************************************
拉宾米勒算法测试素数
调用方式:Rab(N)
返回值:若N为素数,返回1,否则返回0
****************************************************************************************/
static int Rab(CBigInt *N)
{
CBigInt S = {0}, A = {0}, I = {0}, K = {0};
uint32_t i, j, pass;
for(i = 0; i < 550; i++)
{
if(Mod_Big_Long(N, PrimeTable[i]) == 0)
{
return 0;
}
}
memcpy(&K, N, sizeof(CBigInt));
K.m_ulValue[0]--;
for(i = 0; i < 5; i++)
{
pass = 0;
Mov_Big_Long(&A, rand()*rand());
memcpy(&S, &K, sizeof(CBigInt));
while((S.m_ulValue[0] & 1) == 0)
{
for(j = 0; j < S.m_nLength; j++)
{
S.m_ulValue[j] = S.m_ulValue[j] >> 1;
if(S.m_ulValue[j + 1] & 1)
{
S.m_ulValue[j] = S.m_ulValue[j] | 0x8000;
}
}
if(S.m_ulValue[S.m_nLength - 1] == 0)
{
S.m_nLength--;
}
memcpy(&I, &A, sizeof(CBigInt));
RsaTrans(&I, &S, N);
if(Cmp(&I, &K) == 0)
{
pass = 1;
break;
}
}
if((I.m_nLength == 1) && (I.m_ulValue[0] == 1))
{
pass = 1;
}
if(pass == 0)
{
return 0;
}
}
return 1;
}
/****************************************************************************************
产生随机素数
调用方法:GetPrime(N,bits)
返回值:N,被赋值为一个bits位(0x100000000进制长度)的素数
****************************************************************************************/
static CBigInt *GetPrime(CBigInt *N, int bits)
{
uint32_t i;
CBigInt S = {0}, A = {0}, I = {0}, K = {0};
memset(N, 0, sizeof(CBigInt));
N->m_nLength = bits;
begin:
srand(portable_rand_seed());
for(i = 0; i < N->m_nLength; i++)
{
N->m_ulValue[i] = rand() * 0x100 + rand();
}
N->m_ulValue[0] = N->m_ulValue[0] | 1;
for(i = N->m_nLength - 1; i > 0; i--)
{
N->m_ulValue[i] = N->m_ulValue[i] << 1;
if(N->m_ulValue[i - 1] & 0x8000)
{
N->m_ulValue[i]++;
}
}
N->m_ulValue[0] = N->m_ulValue[0] << 1;
N->m_ulValue[0]++;
for(i = 0; i < 550; i++)
{
if(Mod_Big_Long(N, PrimeTable[i]) == 0)
{
goto begin;
}
}
memcpy(&K, N, sizeof(CBigInt));
K.m_ulValue[0]--;
for(i = 0; i < 5; i++)
{
Mov_Big_Long(&A, rand()*rand());
memcpy(&S, &K, sizeof(CBigInt));
Div_Big_Long(&S, 2);
memcpy(&I, &A, sizeof(CBigInt));
RsaTrans(&I, &S, N);
if(((I.m_nLength != 1) || (I.m_ulValue[0] != 1)) && (Cmp(&I, &K) != 0))
{
goto begin;
}
}
return N;
}
/***********************************************************************/
static void entropy_poll(unsigned char *output, unsigned int len)
{
if(len > 0)
{
int i;
srand(portable_rand_seed);
for(i = 0; i < len; i++)
{
output[i] = rand() % 0xff + 1;
}
}
}
static char *del_PKCS1Padding(char *src)
{
int len = strlen(src);
if(len % 2 == 1)
{
src++;
}
while(*src != 0 && *(src + 1) != 0)
{
if(*src == '0' && *(src + 1) == '0')
{
src += 2;
break;
}
src += 2;
}
return src;
}
static int add_PKCS1Padding(unsigned char *src, unsigned int len, unsigned char *out)
{
if(len > RSA_ENCODE_LEN - 11)
{
return -1;
}
else
{
/*要加密的msg*/
memcpy(&out[RSA_ENCODE_LEN - len], src, len);
out[0] = 0;
out[1] = 2;
/*至少8字节的随机数*/
entropy_poll(&out[2], RSA_ENCODE_LEN - 3 - len);
out[RSA_ENCODE_LEN - len - 1] = 0;
return 0;
}
}
static int PKCS1PKCS1PaddingHexRemove(unsigned char *input, unsigned short *len, unsigned char *output)
{
if(input[0] == 0 && (input[1] == 1 || input[1] == 2))
{
int i;
for(i = 2; i < *len; i++)
{
if(input[i] == 0)
{
*len -= (i + 1);
memcpy(output, &input[i + 1], *len);
return *len;
}
}
}
return -1;
}
int RSA2048_pri_PKCS1Padding_Encode(unsigned char *data, unsigned short len, unsigned char *out, char *publicKey, char *ModulusHex)
{
unsigned char buf[RSA_ENCODE_LEN];
CBigInt N, E;
CBigInt mw, mi, jm;
uint16_t outlen = RSA_ENCODE_LEN;
//Get(&N, Modulus, 16);//string
GetHex(&N, ModulusHex, RSA_ENCODE_LEN, 16);//hex array
Get(&E, publicKey, 16);
add_PKCS1Padding(data, len, buf);
GetHex(&mw, buf, RSA_ENCODE_LEN, 16);
RsaTrans(&mw, &E, &N);
PutHex(&mw, out, &outlen);
return outlen;
}
int RSA2048_pub_PKCS1Padding_Encode(unsigned char *data, unsigned short len, unsigned char *out, char *publicKey, unsigned char *ModulusHex)
{
unsigned char buf[RSA_ENCODE_LEN];
CBigInt N, E;
CBigInt mw, mi, jm;
uint16_t outlen = RSA_ENCODE_LEN;
GetHex(&N, ModulusHex, RSA_ENCODE_LEN, 16);//hex array
Get(&E, publicKey, 16);
add_PKCS1Padding(data, len, buf);
GetHex(&mw, buf, RSA_ENCODE_LEN, 16);
RsaTrans(&mw, &E, &N);
PutHex(&mw, out, &outlen);
return outlen;
}
int RSA2048_pri_PKCS1Padding_Decode(unsigned char *data, unsigned short *len, unsigned char *out, char *privateKey, char *ModulusHex)
{
unsigned char buf[RSA_ENCODE_LEN];
CBigInt N, D;
CBigInt mw, jm;
//Get(&N, Modulus, 16);//string
GetHex(&N, ModulusHex, RSA_ENCODE_LEN, 16);//hex array
Get(&D, privateKey, 16);
GetHex(&mw, data, *len, 16);
RsaTrans(&mw, &D, &N);
PutHex(&mw, buf, len);
PKCS1PKCS1PaddingHexRemove(buf, len, out);
return 0;
}
int RSA2048_pub_PKCS1Padding_Decode(unsigned char *data, unsigned short *len, unsigned char *out, char *privateKey, unsigned char *ModulusHex)
{
unsigned char buf[RSA_ENCODE_LEN];
CBigInt N, D;
CBigInt mw, jm;
int t_len = 0;
GetHex(&N, ModulusHex, RSA_ENCODE_LEN, 16);
Get(&D, privateKey, 16);
GetHex(&mw, data, *len, 16);
RsaTrans(&mw, &D, &N);
PutHex(&mw, buf, len);
t_len = PKCS1PKCS1PaddingHexRemove(buf, len, out);
return t_len;
}
//test
static const unsigned char base64_table[65] = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/";
//需要释放内存
unsigned char * base64_encode(const unsigned char *src, size_t len, size_t *out_len)
{
unsigned char *out, *pos;
const unsigned char *end, *in;
size_t olen;
int line_len;
olen = len * 4 / 3 + 4; /* 3-byte blocks to 4-byte */
olen += olen / 72; /* line feeds */
olen++; /* nul termination */
if(olen < len)
{
return NULL; /* integer overflow */
}
out = portable_malloc(olen);
if(out == NULL)
{
return NULL;
}
end = src + len;
in = src;
pos = out;
line_len = 0;
while(end - in >= 3)
{
*pos++ = base64_table[in[0] >> 2];
*pos++ = base64_table[((in[0] & 0x03) << 4) | (in[1] >> 4)];
*pos++ = base64_table[((in[1] & 0x0f) << 2) | (in[2] >> 6)];
*pos++ = base64_table[in[2] & 0x3f];
in += 3;
line_len += 4;
if(line_len >= 72)
{
*pos++ = '\n';
line_len = 0;
}
}
if(end - in)
{
*pos++ = base64_table[in[0] >> 2];
if(end - in == 1)
{
*pos++ = base64_table[(in[0] & 0x03) << 4];
*pos++ = '=';
}
else
{
*pos++ = base64_table[((in[0] & 0x03) << 4) |
(in[1] >> 4)];
*pos++ = base64_table[(in[1] & 0x0f) << 2];
}
*pos++ = '=';
line_len += 4;
}
if(line_len)
{
*pos++ = '\n';
}
*pos = '\0';
if(out_len)
{
*out_len = pos - out;
}
return out;
}
//需要释放内存
unsigned char * base64_decode(const unsigned char *src, size_t len,
size_t *out_len)
{
unsigned char dtable[256], *out, *pos, block[4], tmp;
size_t i, count, olen;
int pad = 0;
memset(dtable, 0x80, 256);
for(i = 0; i < sizeof(base64_table) - 1; i++)
{
dtable[base64_table[i]] = (unsigned char) i;
}
dtable['='] = 0;
count = 0;
for(i = 0; i < len; i++)
{
if(dtable[src[i]] != 0x80)
{
count++;
}
}
if(count == 0 || count % 4)
{
return NULL;
}
olen = count / 4 * 3;
pos = out = portable_malloc(olen);
if(out == NULL)
{
return NULL;
}
count = 0;
for(i = 0; i < len; i++)
{
tmp = dtable[src[i]];
if(tmp == 0x80)
{
continue;
}
if(src[i] == '=')
{
pad++;
}
block[count] = tmp;
count++;
if(count == 4)
{
*pos++ = (block[0] << 2) | (block[1] >> 4);
*pos++ = (block[1] << 4) | (block[2] >> 2);
*pos++ = (block[2] << 6) | block[3];
count = 0;
if(pad)
{
if(pad == 1)
{
pos--;
}
else if(pad == 2)
{
pos -= 2;
}
else
{
/* Invalid padding */
portable_free(out);
return NULL;
}
break;
}
}
}
*out_len = pos - out;
return out;
}
int main(int argc, char *argv[])
{
//原始公钥-私钥
/*
-----BEGIN PUBLIC KEY-----
MIIBIjANBgkqhkiG9w0BAQEFAAOCAQ8AMIIBCgKCAQEAwmejRhw/SB2xB3rgJYhg
OWBDX/DponDVVPzTWhn3J4INv6jUa9HDkeHhys4OOZTNajr8kRy4TIemotnIYONJ
noW7VyIQEAkEyxcMett5mqRPBLuyc8Fygn4ho/rd9JId4+PgKLmr6NVcuZCpVXPe
gyqNx0nR/UojISbq/Bu+NlcStmicZUuAeVbkGGUOlvtMzFehkBPwE31EdpYUq+/z
LuJ8OaxC+zm5PFo2AZJfI5Gz5lgb1g5ud0TG1JUrm9Dl5/JSNSL3SXBEC77mdfd0
BA5VFl8lV7IfTfSTUE9IKoMevqZxoaGpyN+ZcBby5NgsoqJJ6vmcJRFjI92UrFHV
1wIDAQAB
-----END PUBLIC KEY-----
-----BEGIN PRIVATE KEY-----
MIIEvQIBADANBgkqhkiG9w0BAQEFAASCBKcwggSjAgEAAoIBAQDCZ6NGHD9IHbEH
euAliGA5YENf8OmicNVU/NNaGfcngg2/qNRr0cOR4eHKzg45lM1qOvyRHLhMh6ai
2chg40mehbtXIhAQCQTLFwx623mapE8Eu7JzwXKCfiGj+t30kh3j4+Aouavo1Vy5
kKlVc96DKo3HSdH9SiMhJur8G742VxK2aJxlS4B5VuQYZQ6W+0zMV6GQE/ATfUR2
lhSr7/Mu4nw5rEL7Obk8WjYBkl8jkbPmWBvWDm53RMbUlSub0OXn8lI1IvdJcEQL
vuZ193QEDlUWXyVXsh9N9JNQT0gqgx6+pnGhoanI35lwFvLk2Cyioknq+ZwlEWMj
3ZSsUdXXAgMBAAECggEAEnEUaw0475VpesUsSEM0pZy9J3fKIg/EHQjS3+RAru3G
ch0I8aV3gPpFmiCL9uhnyCEKXpWz4gaoRyCTwqUtEa2sBOsFTRAd9Uodc/YoBgR6
Pn+zwQlj3H8sn8qnjZDi5wBx/ksGxNKgtjXD6ohQXm8F/hbBpd6HkJiJiBr1o1/a
4Kzh9L1OpYVS5QF0EN3idNkt911vfjA+bqBXXjAf9IHvirQ2GeCNzmHygxiRhAWA
ki2fm0pGbKFUAfo+sgtDPT2jrA4rhSHG4mMr8IWBpr082aKNns7ujxT9ndBCl0Pp
7efPNCT4+zqfyVAB6x2rYhtXTqR7wsASMIfSLzyoIQKBgQDi2sb9z4OEl0mTV0Ey
1Lia4F06QhD7Kl1mhBWYPA1RO1ieAHHINFvwPJQLjHR2yMRMDmTOc3S9Hy3H3QMG
XZlrIl5sgeFzsdqGyd2kscGFUGkH9RY2V/XB0mxQFIGI2PBztqd6e6BJQz4oSyMz
cBZq/NH5u95QRlyI0I1u5b5lMQKBgQDbYZdhqHcDYmc61aHRNEhnxbK4ph1bdTiM
QbIF0wUssXQKwEzvYzswRlI27rXeSHpJA8vc+XAoD/+Ut30I8Td3yUnnsHZctU2D
b/8OTqwFqyrwXM+SvyWZejuvX6IVJuRwPMFG88L88lryEs0ntlQKC/x6wxtcs67X
6ZGsLSfJhwKBgQDAo09/kIv6OA4+lEXFSGZK/mOsaRXKcztFJry/vZ8BcAfchDwa
6nt4EbkV5XuwsuQeQcrQlbJ4NtXFdqRu72SsWU8djV1Jxanv89PHWzseXh4Sp8jo
9OC4aluX1RH6h14IpP6rP/fovrU1ujh2IaSnzXDxRNuQB2/krlSr62Q2wQKBgGNL
jbgvBwcqH+06So6lKmyFx/nZfgoqSVj6VzhZpcrv2sUO+wOTF3QnMAkbDIg6p9aq
eDhhUklfzF+kmVxVybRXEDNk5H3bteTa6Uexhhzet4WpjG4wRDVuZNtg3rzSKK1A
Yn7Z0BSrIUzWA7OIzArsF+/8pULVNTsWxc93dL27AoGAT3eaPv07rhzyztxFYTsr
dHcgNb+vwroN3Ic7IJnxoa2BjyqczaAG3vMrOcxFg2MLJ7fPmI1W4pPOJyxmUhO0
mZhk+F7h+dg7XB7h0lqR1usp3Ak3qyu1f4XZj4imzQWWyETpgE4uA9tBniPQIRK6
miXhZ2YoXfdsSZOatWojGLI=
-----END PRIVATE KEY-----
*/
//https://www.oren.net.cn/rsa/info.html
//在线转换为模数和指数
//PEM->模数+指数
char *publicKey_exponent = "10001";
char *privateKey_exponent = "1271146b0d38ef95697ac52c484334a59cbd2777ca220fc41d08d2dfe440aeedc6721d08f1a57780fa459a208bf6e867c8210a5e95b3e206a8472093c2a52d11adac04eb054d101df54a1d73f62806047a3e7fb3c10963dc7f2c9fcaa78d90e2e70071fe4b06c4d2a0b635c3ea88505e6f05fe16c1a5de87909889881af5a35fdae0ace1f4bd4ea58552e5017410dde274d92df75d6f7e303e6ea0575e301ff481ef8ab43619e08dce61f2831891840580922d9f9b4a466ca15401fa3eb20b433d3da3ac0e2b8521c6e2632bf08581a6bd3cd9a28d9eceee8f14fd9dd0429743e9ede7cf3424f8fb3a9fc95001eb1dab621b574ea47bc2c0123087d22f3ca821";
//hex array ,faster than string
//直接使用16进制数据可略微提高速度,软件也支持传入字符串
// 具体看代码中 GetHex 和 Get
static unsigned char ModulusHex[RSA_ENCODE_LEN] =
{
0xC2, 0x67, 0xA3, 0x46, 0x1C, 0x3F, 0x48, 0x1D, 0xB1, 0x07, 0x7A, 0xE0, 0x25, 0x88, 0x60, 0x39,
0x60, 0x43, 0x5F, 0xF0, 0xE9, 0xA2, 0x70, 0xD5, 0x54, 0xFC, 0xD3, 0x5A, 0x19, 0xF7, 0x27, 0x82,
0x0D, 0xBF, 0xA8, 0xD4, 0x6B, 0xD1, 0xC3, 0x91, 0xE1, 0xE1, 0xCA, 0xCE, 0x0E, 0x39, 0x94, 0xCD,
0x6A, 0x3A, 0xFC, 0x91, 0x1C, 0xB8, 0x4C, 0x87, 0xA6, 0xA2, 0xD9, 0xC8, 0x60, 0xE3, 0x49, 0x9E,
0x85, 0xBB, 0x57, 0x22, 0x10, 0x10, 0x09, 0x04, 0xCB, 0x17, 0x0C, 0x7A, 0xDB, 0x79, 0x9A, 0xA4,
0x4F, 0x04, 0xBB, 0xB2, 0x73, 0xC1, 0x72, 0x82, 0x7E, 0x21, 0xA3, 0xFA, 0xDD, 0xF4, 0x92, 0x1D,
0xE3, 0xE3, 0xE0, 0x28, 0xB9, 0xAB, 0xE8, 0xD5, 0x5C, 0xB9, 0x90, 0xA9, 0x55, 0x73, 0xDE, 0x83,
0x2A, 0x8D, 0xC7, 0x49, 0xD1, 0xFD, 0x4A, 0x23, 0x21, 0x26, 0xEA, 0xFC, 0x1B, 0xBE, 0x36, 0x57,
0x12, 0xB6, 0x68, 0x9C, 0x65, 0x4B, 0x80, 0x79, 0x56, 0xE4, 0x18, 0x65, 0x0E, 0x96, 0xFB, 0x4C,
0xCC, 0x57, 0xA1, 0x90, 0x13, 0xF0, 0x13, 0x7D, 0x44, 0x76, 0x96, 0x14, 0xAB, 0xEF, 0xF3, 0x2E,
0xE2, 0x7C, 0x39, 0xAC, 0x42, 0xFB, 0x39, 0xB9, 0x3C, 0x5A, 0x36, 0x01, 0x92, 0x5F, 0x23, 0x91,
0xB3, 0xE6, 0x58, 0x1B, 0xD6, 0x0E, 0x6E, 0x77, 0x44, 0xC6, 0xD4, 0x95, 0x2B, 0x9B, 0xD0, 0xE5,
0xE7, 0xF2, 0x52, 0x35, 0x22, 0xF7, 0x49, 0x70, 0x44, 0x0B, 0xBE, 0xE6, 0x75, 0xF7, 0x74, 0x04,
0x0E, 0x55, 0x16, 0x5F, 0x25, 0x57, 0xB2, 0x1F, 0x4D, 0xF4, 0x93, 0x50, 0x4F, 0x48, 0x2A, 0x83,
0x1E, 0xBE, 0xA6, 0x71, 0xA1, 0xA1, 0xA9, 0xC8, 0xDF, 0x99, 0x70, 0x16, 0xF2, 0xE4, 0xD8, 0x2C,
0xA2, 0xA2, 0x49, 0xEA, 0xF9, 0x9C, 0x25, 0x11, 0x63, 0x23, 0xDD, 0x94, 0xAC, 0x51, 0xD5, 0xD7
};
unsigned char encode_str[RSA_ENCODE_LEN] = {0};
unsigned char decode_str[RSA_ENCODE_LEN] = {0};
int outlen = 0;
unsigned char * base64_str = NULL;
unsigned int base64_str_len = NULL;
uint8_t* decode_base64 = NULL;
char pub_source_string[] = "embedded-system > Public key to RSA encode,hehe";
char pri_source_string[] = "embedded-system > Private key to RSA encode,haha";
printf("RSA demo");
//---------------------------------------------------
memset(encode_str, 0, sizeof(encode_str));
memset(decode_str, 0, sizeof(decode_str));
//公钥加密
outlen = RSA2048_pub_PKCS1Padding_Encode(pub_source_string, strlen(pub_source_string), encode_str, publicKey_exponent, ModulusHex);
//密文转base64方便显示,和在线工具对比结果
// https://the-x.cn/cryptography/Rsa.aspx
//base64_str = base64_encode(encode_str, outlen, &base64_str_len);
//printf("Public encode %d\r\n%s\r\n", base64_str_len, base64_str);
//portable_free(base64_str);
//私钥解密
RSA2048_pri_PKCS1Padding_Decode(encode_str, &outlen, decode_str, privateKey_exponent, ModulusHex);
printf("Private decode %d\r\n%s\r\n", outlen, decode_str);
//---------------------------------------------------
memset(encode_str, 0, sizeof(encode_str));
memset(decode_str, 0, sizeof(decode_str));
//私钥签名
outlen = RSA2048_pri_PKCS1Padding_Encode(pri_source_string, strlen(pri_source_string), encode_str, privateKey_exponent, ModulusHex);
//公钥验签
RSA2048_pub_PKCS1Padding_Decode(encode_str, &outlen, decode_str, publicKey_exponent, ModulusHex);
printf("Public decode %d\r\n%s\r\n", outlen, decode_str);
//---------------------------------------------------
printf("RSA demo done");
return 0;
}5、应用
和AES一样,RSA也是块加密算法( block cipher algorithm),只针对固定长度明文,如RSA2048其加密的数据长度需要填充后是2048位即256字节,如果明文长度大于256字节则需要拆分。当然最简单的办法是应用层分配256字节缓存,有效数据以外以0x00填充。
RSA算法虽然安全,但其计算量非常大,效率较低,尤其在嵌入式系统中,硬件资源有限的情况下加密、解密时间以秒为单位。而对称加密算法AES算法效率高,但其在密钥协商时,在网络传输中有被拦截的风险,或者任一方保存不当导致密钥泄露,其密钥存在很大的安全隐患。
所以,考虑到安全性和高效性,一般采用多种算法组合加密的方式。使用RSA来加密AES的密钥,密钥协商后,使用AES来对后续数据进行加密。




 “人工智能+”行动重磅发布!ElfBoard助力嵌入式教育智能化升级
“人工智能+”行动重磅发布!ElfBoard助力嵌入式教育智能化升级 28nm以下e-flash技术空白?这国产技术填上了!
28nm以下e-flash技术空白?这国产技术填上了!






 慧聪电子网微信公众号
慧聪电子网微信公众号
 慧聪电子网微信视频号
慧聪电子网微信视频号

精彩评论